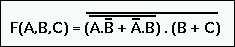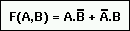- We introduceren twee hulpvariabelen D en E. D is de uitgang van
de EXNOR en E is de uitgang van de OR.
We vinden dan:

Een mogelijke uitdrukking voor F(A,B,C) is:
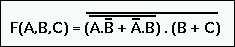
- De waarheidstabel voor de figuur is:
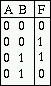
Een uitdrukking voor F(A,B) is:
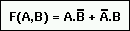
De schakeling is equivalent met een EXOR-poort, zoals uit de waarheidstabel blijkt.
- Een drie-input OR poort geeft een 1 op de uitgang als er een of
meer ingangen 1 zijn. De waarheidstabel is:

- De waarheidstabel van de gegeven functie F(A,B,C,D) is:

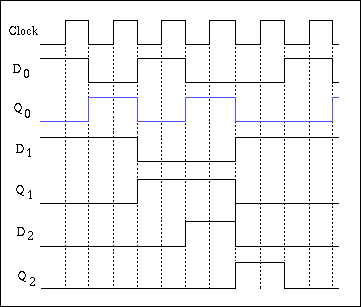
- De schakeling bevat 3 master-slave D-flipflops. De ingangen D0, D1 en
D2 worden op de opgaande clockflank bemonsterd. De uitgangen worden op de
neergaande flank aangepast. Let op: de clock voor flipflip 1 wordt
geleverd door het signaal Q0 (hier blauw weergegeven).
Voor de schakeling vinden we dan:
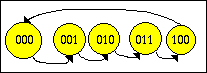
De sequence die deze vijfteller doorloopt is weergegeven in de volgende
figuur:
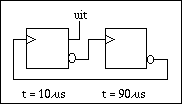
- Door twee monostabiele multivibrators op de juiste wijze in cascade te schakelen
is een astabiele multivibrator met de gewenste dutycycle en frequentie
samen te stellen. Let erop dat steeds een multivibrator actief is. Als de puls
afgelopen is wordt de volgende getriggerd.
- Een waarheidstabel van een 4 naar 1 multiplexer ziet er als volgt uit:
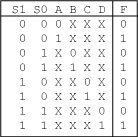
Om te voorkomen dat de tabel erg groot wordt gebruiken we don't
care symbolen voor de ingangen die niet geselecteerd zijn.
In de praktijk kiest men vaak voor een nog compactere weergave. Uit de volgende
tabel (die nu strikt gesproken geen waarheidstabel meer is)
blijkt dat F = A voor de situatie dat beide selectingangen S1 en S0 0 zijn. F = B als S1 = 0 en S0 = 1 etc. De volgende tabel geeft dat weer.

- Om twee getallen van ieder 8 bits op te tellen hebben we nodig:
1 half-adder (voor de twee minst significante bits) en 7 full-adders voor
de resterende bits.
- Deze schakeling is op pagina 82 en 83 uitgewerkt.
Zie figuur 5.14 op bladzijde 82 voor het toestandsdiagram.